We know that this is not true, so from the start we should not expect to end up with the most diversified portfolio over the out-of-sample period. Actually achieving the most diversified portfolio is likely a case of luck, where Sharpe ratios across assets just so happen to align.
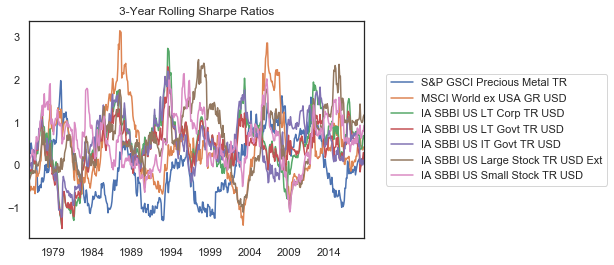
To see this spread more clearly, we can calculate the range of Sharpe ratios at each point. The difference in the proportionality of the return to the volatility goes as high as 3.5 and dips down below 1. However, it is never zero.
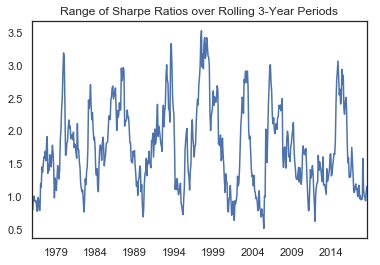
Optimal portfolios aside, getting close to the maximum diversification portfolio ex-post would still be a win for the method and a show of robustness.
For comparison, assume for a moment that we still held the same views about portfolio construction but removed the active views on correlation. This leads to inverse volatility weighting the portfolio (naïve risk parity).
The following chart compares these two portfolios as a fraction of realized range of potential diversification ratios. For example, if the maximum diversification ratio was 3 and the minimum was 1, a realized diversification ratio of 2.5 would correspond to a fraction of 75% of the possible range.
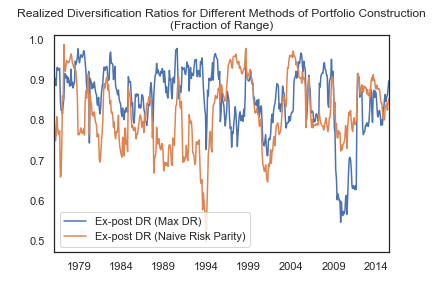
As a testament to its robustness, the median position of the diversification ratio for the maximum diversification portfolio within the potential range was 87%.
The maximum diversification portfolio led to a higher diversification ratio than that of the naïve risk parity portfolio in 65% of the rolling periods. During the Financial Crisis and Tech Bubble, when correlations climbed the most, both methods showed less diversification – an important reminder that correlations are not a law.
What About Returns?
While the maximum diversification portfolio requires no active views on returns, this may be the area that would make investors hesitate before adopting this method of portfolio construction, especially if they are not willing to employ leverage.
Over the test period, the maximum diversification portfolio has been similar to a conservative 25/75 stock/bond allocation.
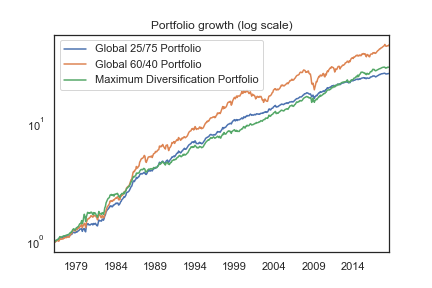
Its maximum drawdown of 13% compared to 11% for the 25/75 demonstrates diversification-based risk management (the 60/40 had a maximum drawdown of 32%). It did experience periods in the 70s and 80s when it outperformed simple strategic allocations, but with an annualized tracking error of 6%, this performance difference can cut both ways.
Assuming that your beliefs about correlations, volatilities, and returns align with those needed for the maximum diversification portfolio, three uses of this technique are:
- Combine it with leverage and other portfolio construction techniques (for mitigating estimation risk) to target a specific volatility.
- Use it to construct a conservative portfolio that requires careful management of sequence risk.
- Use it as a benchmark for assessing diversification within an existing portfolio and considering tactical tilts to improve the diversification ratio.
Conclusion
Like all portfolio construction techniques, the calculation of the most diversified portfolio requires a set of assumptions that are not often met by out-of-sample data. It does not entail as much estimation risk as mean-variance optimization, as it does not require estimates of asset returns.
It can generate a Sharpe optimal portfolio if Sharpe ratios are constant for all assets, but since this is rarely the case, it is probably best to treat it as simply another portfolio construction technique in the quantitative toolbox for managing uncertainty in estimation.
Beyond that, the most diversified portfolio is somewhat of an idealized target but is not generally in line with the objectives of most investors. It could be directly useful in some isolated cases, but its true value comes from the information it provides about what level of diversification is possible in a given investment universe.
Through the diversification ratio, we can see how diversified a portfolio is and the theoretical maximum value that could have been achieved.
With the pursuit of diversification already at odds with how investors evaluate portfolios in hindsight, finding the correct level of diversification is probably more important than maximizing it.
1. Choueifaty, Yves, and Yves Coignard. 2008. “Toward Maximum Diversification.” Journal of Portfolio Management 35 (1). http://www.tobam.fr/wp-content/uploads/2014/12/TOBAM-JoPM-Maximum-Div-2008.pdf: 40–51.

