By Karl Steiner
I don’t often write about “volatility” here at Mindfully Investing because mindful investors focus on long-term returns more than the routine ups and downs of the markets. The standard deviation of return sequences is the most common measure of routine volatility for stocks, bonds, and other asset classes. But as I explained in a previous post, standard deviation is actually a poor measure of the potential for a permanent loss, which is the risk that matters most to real-life investors. A permanent loss is when your invested money is not available at the time you expected to spend it, such as when retirement begins.
Despite all that, I thought it was time to write more about volatility because 2020 was the second most volatile year for stocks in the last 50 years. (Only the historic and brief crash of 1987 involved more stock volatility in a single year.) Perhaps, you thought about selling your stocks in March 2020, when the S&P 500 was down nearly -35% as shown in this graph.
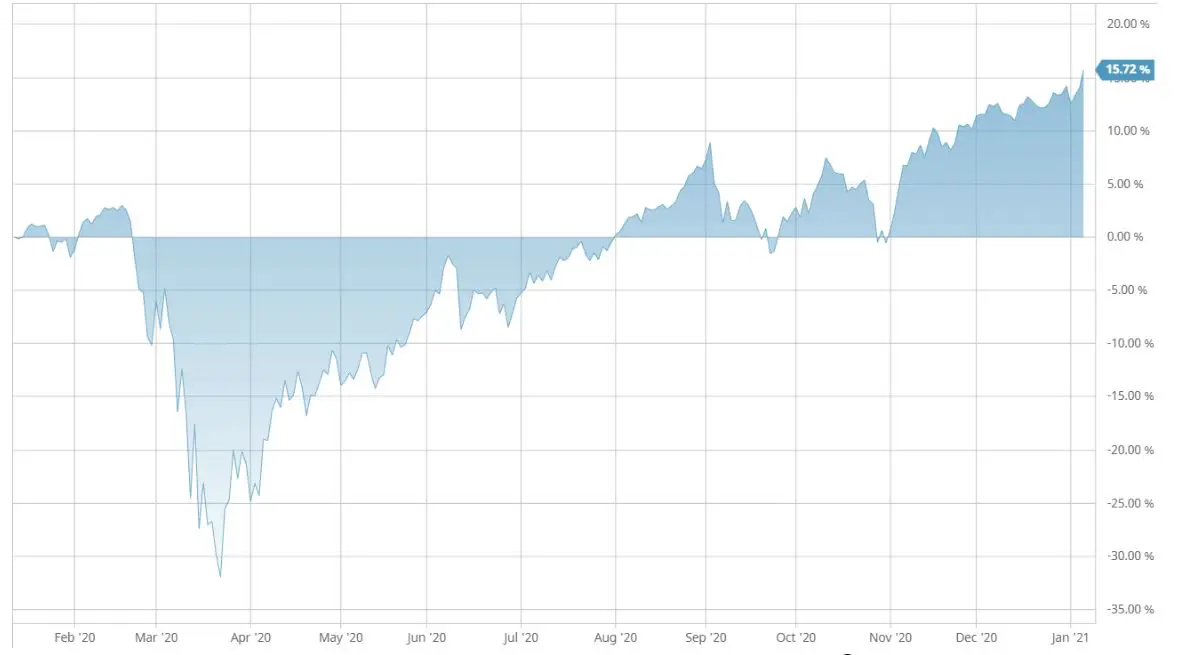
But if you resisted the urge to sell, you only had to wait four short months until all that “lost” money was back in your investing account like magic.
And investors in the S&P 500 who waited until the end of the year found that Santa had left 15% more money in their accounts as compared to the start of 2020! That’s almost double the typical annualized return for stocks going back to 1887. More than any other year since I started investing, 2020 has made it crystal clear that routine volatility does not equate to the risk of permanent loss.
And a brief review of a few common fallacies about volatility highlights some other reasons why volatility is a poor measure of risk.
Fallacy 1: More Volatility Means Higher Potential Returns
You may have noticed that asset classes with higher potential returns tend to be more volatile; they exhibit higher standard deviations. I’ve previously pointed out the fairly consistent relationship between return and volatility when comparing the multi-decade histories of broad asset classes like stocks, bonds, and cash as shown in this graph.
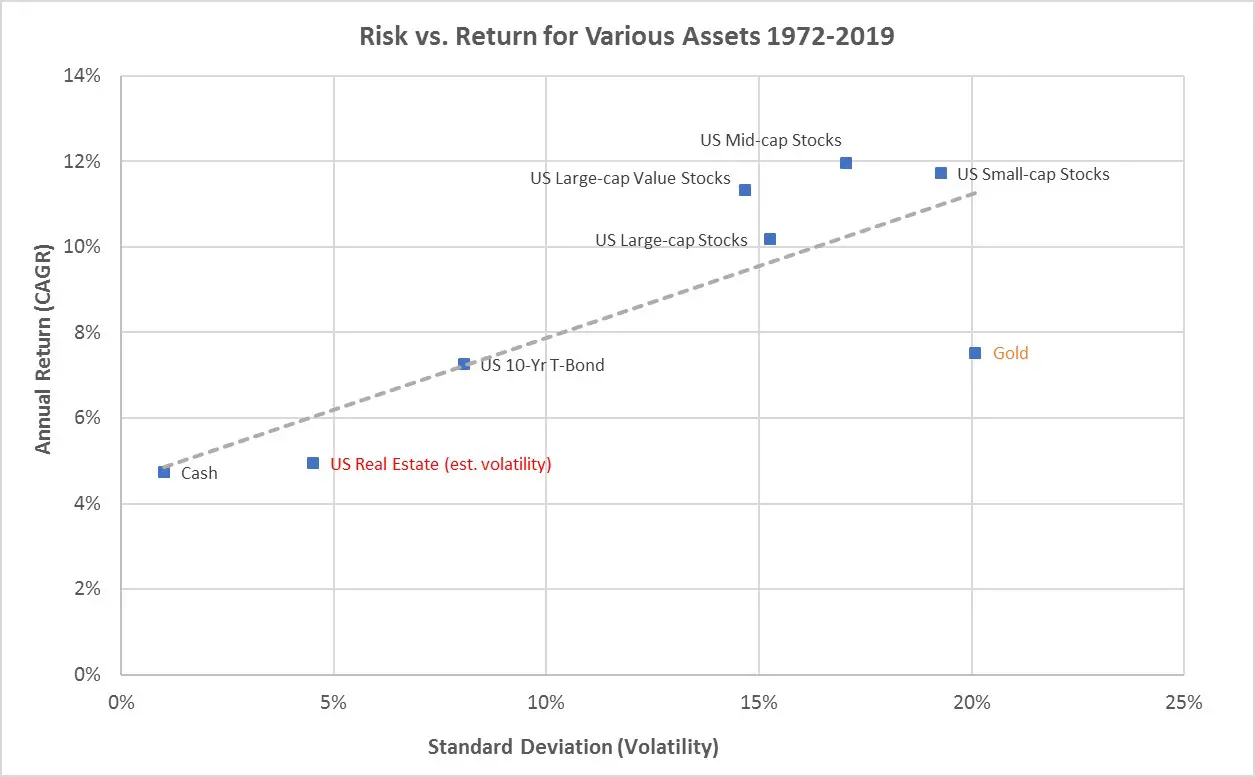
But this long-term relationship amongst asset classes fails to describe the more routine interplay of volatility and returns within individual asset classes or individual portfolios.
Vanguard provides a good example in this graph of volatility as a sequence of returns plays out.
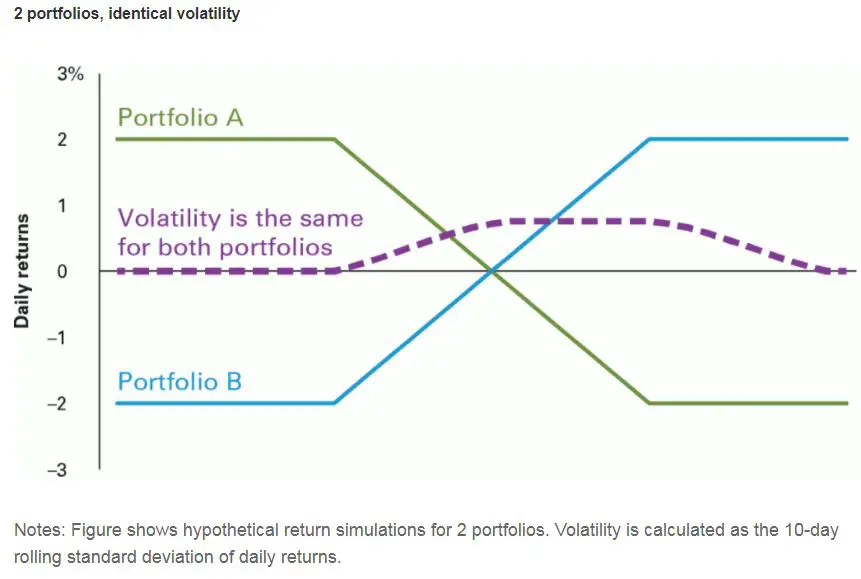
Volatility (purple dashed line) as measured by the standard deviation is the same for fictional Portfolios A and B at each point in time. But Portfolio A has accumulated losses, while Portfolio B has accumulated gains. Because volatility measures deviations in both positive and negative returns, volatility alone indicates very little about the potential for positive returns over time.
Fallacy 2: More Volatility Means More Severe Potential Losses
The risk of losses (negative returns) is probably the main reason that most investors pay attention to volatility statistics. But this doesn’t mean that more volatility necessarily leads to greater losses as this example graph from Investopedia shows.
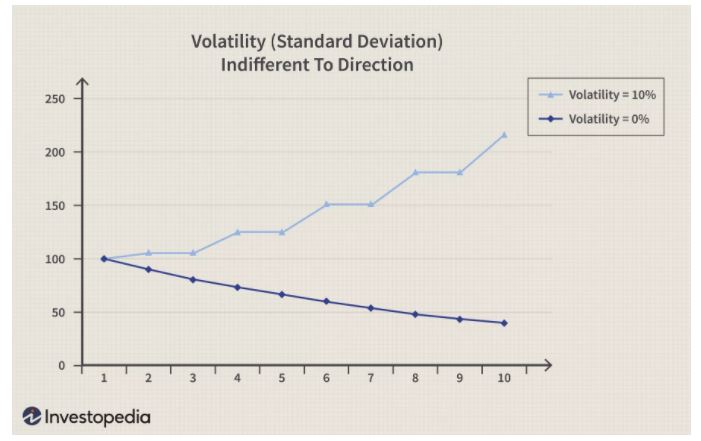
The returns of the fictional stock shown in light blue are positive in an erratic fashion. Academics would say that the stock shows “dispersion”. For the light blue stock, dispersion generates 10% volatility. But the returns of the fictional portfolio shown in dark blue decline without dispersion, which generates 0% volatility. Clearly, the dark blue stock is a worse investment than the light blue stock, but again, you wouldn’t know that just by examining volatility.
Fallacy 3: Returns and Volatility Are Correlated
The graph at the top of today’s post shows that more volatile asset classes have often generated higher returns when viewed over many decades. This observation has fostered another fallacy that returns and volatility should be correlated within asset classes over shorter periods like weeks, months, or years. And given that volatility measures deviations in both positive and negative directions, one might imagine a perfect short-term correlation with returns would look something like this graph.
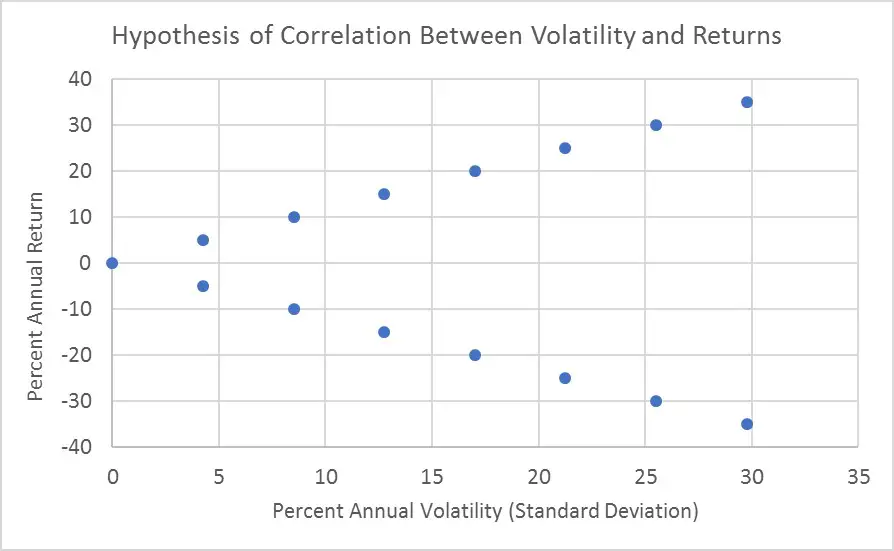
The hypothesis is that in some years increased volatility happens due to market crashes, causing losses. But in other years increased volatility happens due to market bubbles, which causes impressive gains. Thus, we get the supposed v-shape depicted above.
However, a plot of actual S&P 500 annual nominal (not inflation-adjusted) return and volatility data going back to 1972 from Portfolio Visualizer clearly refutes the idea that these two measures are correlated within asset classes on smaller timescales.
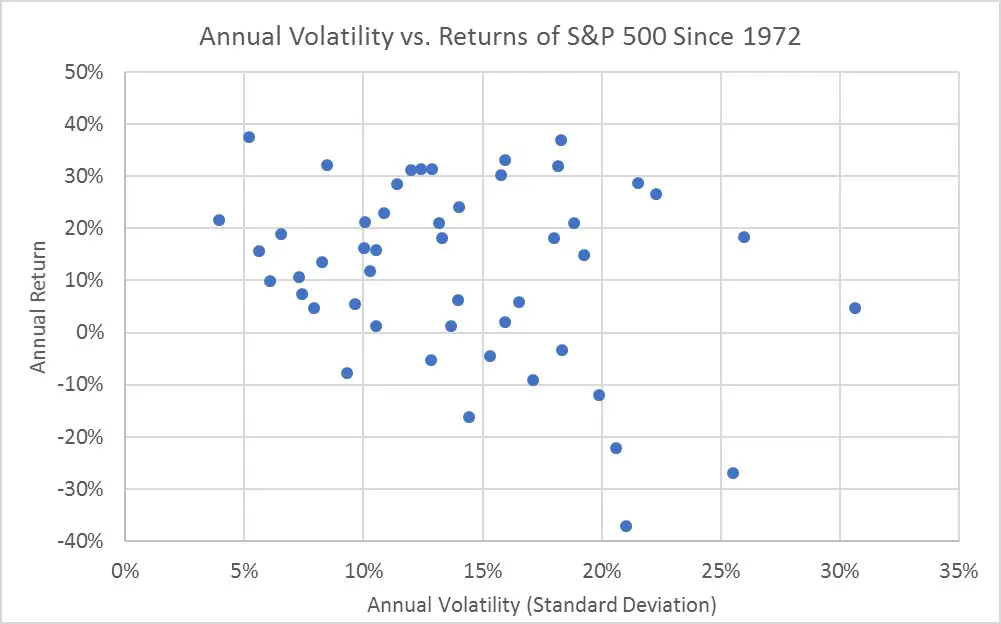
I suppose if you squint really hard you might see a v-shape, but I certainly don’t. However, let’s take a closer look by separating years of positive returns and negative returns as shown in these two graphs.
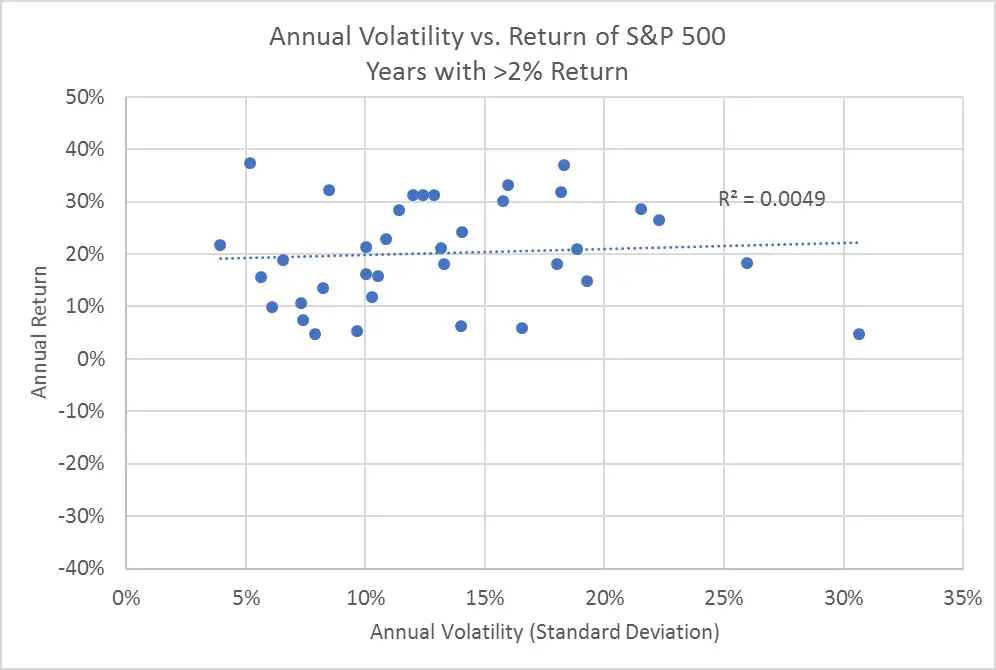
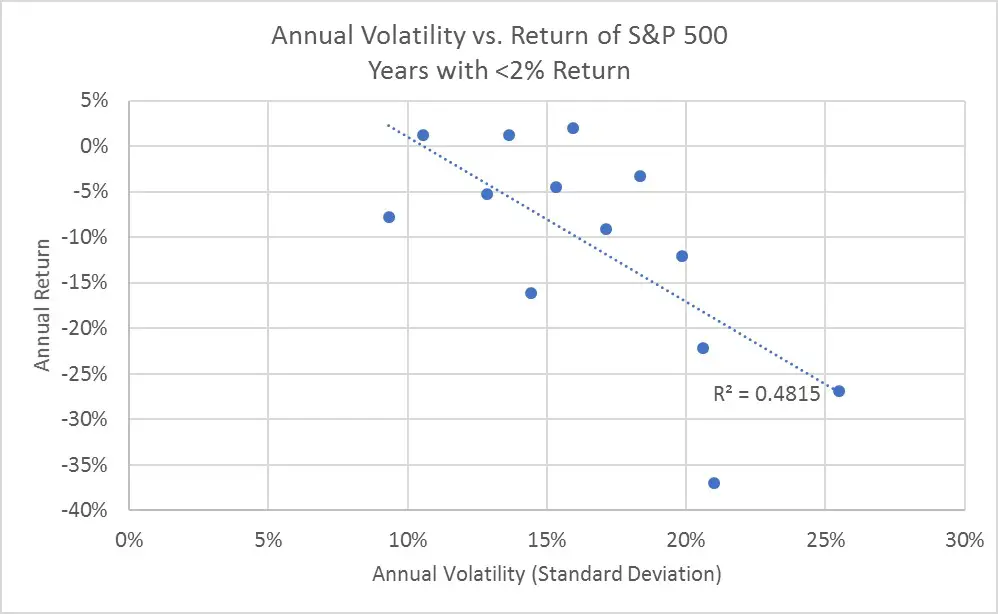
The first thing to note about these two graphs is that I assigned years to the “positive” upper graph when the annual return was above 2% nominal and years to the “negative” lower graph when the annual return was below that same level. I used this 2% threshold because it showed the highest correlation for the “negative” return years. That may sound arbitrary, but a return of less than about 2% nominal is firmly below the annualized inflation rate of 3.9% over this same period. So, values below a 2% nominal return reflect inflation-adjusted (real) losses in all these years.
The very low r-squared value of 0.005 on the top graph shows that there’s no correlation between volatility and returns in positive return years. But the r-square value of 0.48 on the bottom graph shows there’s a decent correlation between these measures in negative return years. So, the fallacy of short-term correlation between volatility and returns is not entirely wrong, but it needs some clarification. Specifically, if history is any guide, there’s a reasonable expectation that, during times of market turmoil, declining stock prices will be associated with higher volatility.
Better Measures of Volatility?
The S&P annual volatility data suggest that standard deviation may not effectively measure the risk of negative returns, which is the volatility that most investors care about. Standard deviation captures all the noisy data from the positive return years, which may drown out the moderate correlation from the negative years.
For this and other reasons, many people think that a better measure of volatility is something called “downside deviation”. You can learn more about the calculation of downside deviation here. Essentially, downside deviation accounts for volatility only when returns occur below a specified level. Like my example above, you could specify that level as 2% nominal. Or you could choose another level such as the risk-free rate of return or the rate of inflation for the same period.
So, what’s the downside deviation for the S&P 500? Although Portfolio Visualizer doesn’t provide downside deviation, I calculated that value from other statistics provided by Portfolio Visualizer. (These particular statistics appear to use the risk-free rate of return as the downside threshold.)
- The downside deviation for the S&P 500 from 1972 to 2000 was 9.2%.
Unfortunately, you can’t compare this number directly to standard deviation, because it’s calculated slightly differently. Instead, I calculated the “upside deviation” for the same data set using the mirror identical calculation.
- The upside deviation for the S&P 500 from 1972 to 200 was 16.8%.
So, the upside deviation is almost twice the downside deviation. This suggests that almost two-thirds of the observed deviations are due exclusively to years with positive returns.
The Downside to Downside Deviation
It’s tantalizing to think that downside deviation might provide a more efficient measure of the risk of losses. However, I looked at 14 different stock and bond asset classes over varying time periods using Portfolio Visualizer and generated both downside deviations and plain vanilla standard deviations as shown in this graph.
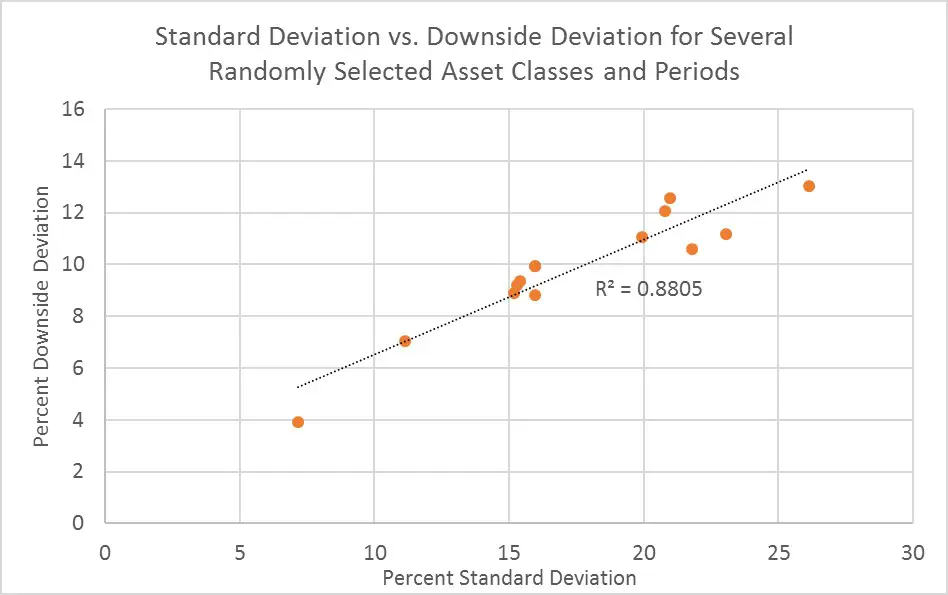
The high r-squared value here of 0.88 indicates that both downside deviation and standard deviation provide very similar answers, but on different scales. Even after 14 tries, I couldn’t find an asset or portfolio where the downside deviation and the standard deviation suggested something entirely different about the risk of losses. I won’t annoy you with a description of every asset and portfolio shown in this graph. But I’ll freely admit that my choice of assets and portfolios was subjectively random, so my analysis is, therefore, not statistically rigorous.
Nonetheless, I see two potential reasons for the similarity between these deviation measures. One, perhaps downside deviation does a poor job of eliminating the upside deviation noise for some reason. Or two, the standard deviation somehow manages to capture the essence of downside deviation despite all the upside noise. I’m not sure which is true, and I may come back to this mystery in later posts. But for now, I suspect that downside deviation fails to isolate the potential for losses any better than the plain vanilla standard deviation.
I previously alluded to the fact that downside deviation is used in other statistics provided by Portfolio Visualizer. The most prominent of these statistics is something called the “Sortino Ratio“. This ratio divides the excess return (the return above the specified threshold) by the downside deviation. Put another way, the Sortino Ratio is one way to calculate a so-called risk-adjusted return. But because downside deviation is the only volatility-related input to this calculation, the Sortino Ratio doesn’t clarify the risk of losses. And I’ve noted before that mindful investors don’t place much significance on risk-adjusted returns for reasons discussed here.
Conclusions
When I started this post, I was kind of hoping to find a better way to measure the risk of losses than the standard deviation, which as we’ve seen, can be misleading on several levels. Unfortunately, the “better” measures I found (downside deviation and its cousin Sortino ratio) don’t seem to reveal anything particularly different from the standard deviation.
This leads me back to the same opinion that I had before I started this post. While volatility can be mesmerizing, particularly in tumultuous years like 2020, it’s still only a sideshow for mindful investors. Regardless, of how we measure volatility, we need to remember that the routine ups and downs of the market don’t determine whether we will incur permanent losses. Of course, for that to be true, we need to remain mindful and resist the urge to sell when events like those of 2020 stoke our fears.
Originally published by Mindfully Investing, 1/7/21
