Summary
- For hedging strategies, there is often a trade-off between degree, certainty, and cost.
- Put options have high certainty and typically offer a high degree of protection, making them costly to hold and roll over the long run.
- In this note, we briefly explore the application of different tactical signals to a 9-month, 25-delta rolling put strategy in an effort to reduce long-term costs.
- We find that signals based upon volatility appear to perform significantly better than signals based upon price changes, likely due, at least in part, to the nature of the put we are purchasing, which has significant sensitivity to changes in implied volatilities.
- These results must be taken with a significant grain of salt due to the low number of actual crisis events to measure against. Furthermore, these results are not applicable for investors for whom a certain degree of loss would be disruptive to their financial plan or needs (e.g. impacting withdrawal / spending plans or forcing the liquidation of assets). For other investors, however, the tactical application of put options may represent an interesting pay-off profile.
In managing risk, there are three primary trade-offs to consider: degree, cost, and certainty.
Degree measures how much protection we are looking too get. Rather than thinking of degree as how much of our portfolio we’re looking to protect (e.g. 10% vs 100% of our notional exposure), we want to think of this more in terms of the loss level we want the protection to begin at. For example, degree captures whether we want to protect against all losses or just losses greater than 30%.
Cost captures how much we must pay for our protection. This cost can be explicit (i.e. we pay a known, up-front premium) or implicit (e.g. whipsaw cost in trend following).
Finally, certainty captures how reliable the hedge is. A centrally cleared put option, for example, has a very high degree of certainty. Buying a call option on Treasury bonds (perhaps to benefit from the materialization of a flight-to-safety trade or as a bet on Fed policy during a crisis) carries with it some basis risk if our primary goal is to protect against equity losses.
Like many trade-offs in life, this is one of those “pick two” cases. You can have a high degree of protection with high reliability, but it will cost you a lot. If you want to reduce the cost, you’ll need to either reduce the degree of protection or the certainty.
Rather than trying to find the holy grail of high degree, high certainty, and low cost, our time is likely better spent first considering the axis by which we are constrained. For example, if a 50% loss represents a catastrophic outcome (e.g. impacting withdrawal / spending plans and potentially having knock-on effects in creating forced asset sales), then we can seek to maximize certainty and minimize cost for this specific scenario. On the other hand, if we cannot afford to spend more than 300 basis points a year on risk management, then we can try to maximize degree and certainty for that budget.
Put options, by definition, have a high degree of certainty, and therefore tend to carry a fairly substantial cost. For example, below we plot the return of a put option strategy that rolls 9-month, 25-delta puts each month, purchasing enough puts to cover 100% of the S&P 500.
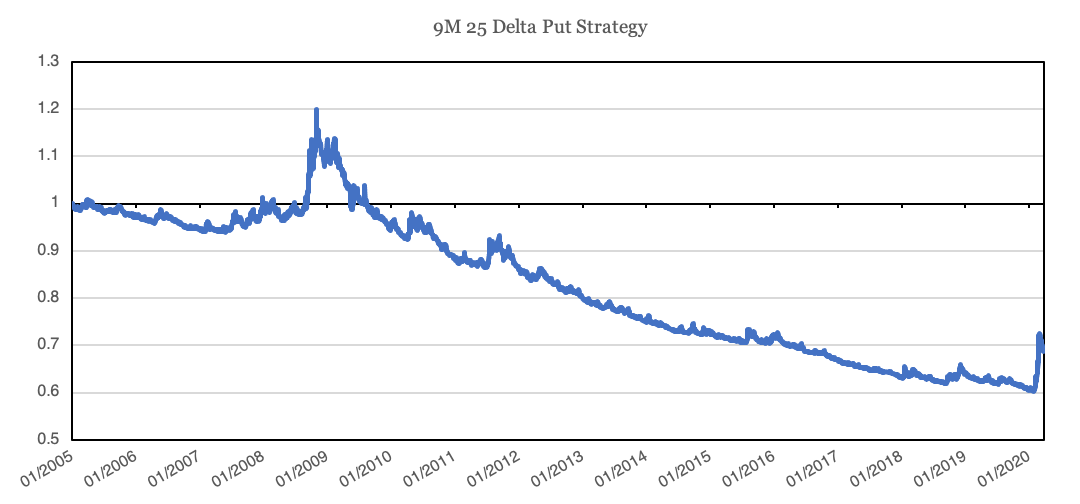
Source: DiscountOptionsData.com. Calculations by Newfound Research. Returns are hypothetical and backtested. Returns are gross of all fees including, but not limited to, management fees, transaction fees, and taxes. Returns assume the reinvestment of all distributions.
Despite offering meaningful returns during the 2008 economic crisis and the recent March 2020 COVID-19 panic, this strategy has still lost -2.3% annualized.
To be fair, this is a very naïve tail hedging strategy. There are no considerations for generating offsetting carry (e.g. a put ratio approach), pro-active monetization, trade conversion (e.g. puts to put spreads), reasonable basis risk trades, or exchanging between linear and non-linear trades.
And it may not be wholly fair to evaluate the returns of a tail risk strategy in isolation. After all, it may help increase the geometric returns of an equity portfolio substantially if appropriately rebalanced.
Nevertheless, this example highlights that if we want to combine a high degree of protection with certainty, it should carry relatively high cost.
In this commentary we will explore a few ideas for dynamically employing put options, attempting to maintain relatively high certainty while minimizing cost.
Tactical Signals
Using tactical signals to identify when to buy put options is akin to waiting to smell smoke before calling your agent to buy fire insurance. It may save significant cost over the long run, but you risk failing to have protection in periods where you cannot get to the phone fast enough or by the time that you do, the cost of insurance is prohibitive.
Nevertheless, in cases where a tail hedge is not necessary (i.e. true knock-out conditions) but simply preferred, tactical tail hedging may provide an attractive payoff.
Below we explore a variety of signals which may indicate elevated risk going forward. At the core of our approach will be the 9-month 25-delta put strategy we introduced above. For each of our signals, when the signal indicates rising risk, we will buy into the put strategy. Otherwise, we will assume a 0% return cash position.
It should be stressed that this is a rather general approach to what can be a highly specific problem for allocators. By rolling far-dated puts each month, our strategy will have exhibit substantial convexity to changes in implied volatility, whereas a short-dated put would exhibit greater convexity to changes in the S&P 500 itself. This means that our approach may not be suitable for protecting against slow, tepid market declines.
Fortunately, market declines and changes in volatility have historically exhibited significant negative correlation. Therefore, for large and rapid declines, we can generally expect the value of our long-dated, deep out-of-the-money puts to appreciate significantly.
Given that our options will be highly sensitive to changes in implied volatility, we explore signals that are not only potentially related to losses in U.S. equities, but also appreciation of expected volatility.
| Indicator | Measure | Thesis |
| S&P 500 Returns | 63-Day Return | Negative returns in the S&P 500 may forecast negative returns going forward. |
| S&P 500 Returns | Z-Score of 63-Day Return (126-Day) | Below average returns in the S&P 500 may forecast negative returns going forward. |
| S&P 500 Trend | 30×120 EWMA | Negative trend signals in the S&P 500 may forecast negative returns going forward. |
| 1M IV | 63-Day Change | Increasing implied volatility may be a sign that investors believe risk is increasing. |
| 1M RV | 63-Day Change | Increasing realized volatility may be a sign that volatility will increase in the future. |
| 1M RV – IV | 63-Day Change | If realized volatility is increasing beyond implied volatility, it may be a sign that protection is underpriced. |
| 1M – 3-Month RV | 63-Day Change | If short-term volatility is higher than medium-term volatility, it may be a sign that risk is increasing. |
| Skew (1M 25 Delta Put – Call) | 63-Day Change | If the skew of the volatility curve is increasing, it may be a sign that investor demand for protection has gone up. |
| Short Volatility Strategy | 63-Day Return | If the return of a short volatility strategy is negative, it may be a sign that risk is increasing. |
| High Yield Credit Spreads | 63-Day Change | If markets are demanding an increasing premium for credit risk, it may be a sign that economic risk is increasing. |
Why would we expect tactical signals to work? The core thesis is partially behavioral and partially structural. On the behavioral side, we expect investors to first under- and then over-react to regime changes in the market. Ideally tactical signals can cue us into these changes before the herd catches on, and then we can benefit as the herd reprices markets.
From a less irrational perspective, we expect investors to exhibit “knock-out” conditions whereby they become forced sellers. For example, as prices fall and volatility picks up, collateral requirements may go up. This can cause forced de-leveraging, further driving down prices and further driving up collateral requirements. This type of positive feedback loop can create liquidity and credit spirals in markets. Therefore, by buying protection at the early signs of a potential market dislocation, we can potentially protect ourselves from the non-economically driven behavior of other market participants.
Note that we focus on fairly short measurement periods. This is for two reasons. First, risk can reprice rapidly, so we want to make sure. Secondly, put options allow us to explicitly measure, per day, how much we’ll pay in premium for the non-linear payoff we are purchasing. This massively asymmetric payoff profile means that we may be able to afford more false positives, unlike trend following where our capital may be meaningfully eroded by whipsaw or jump risk.
Below we plot the returns of applying each signal. When a signal indicates heightened risk (e.g. increasing volatility or declining prices), we purchase the put strategy index. We tranche positions over a 20-trading-day period, meaning that if a signal stays constant, we’ll increase our position by 5% a day. If a signal turns on and then immediately off, we’ll carry at least a 5% position for 20 trading days.
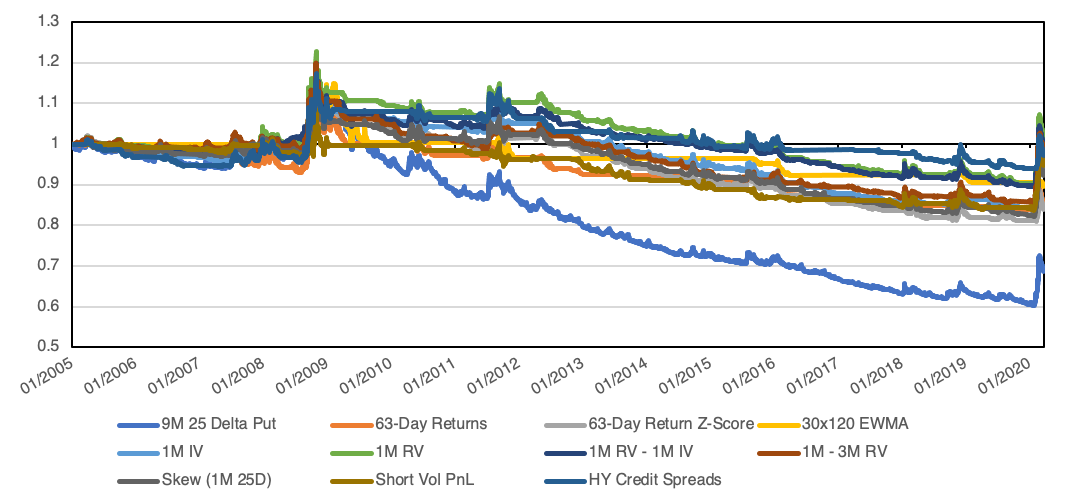
Source: DiscountOptionsData.com; Tiingo.com; St. Louis Federal Reserve. Calculations by Newfound Research. Returns are hypothetical and backtested. Returns are gross of all fees including, but not limited to, management fees, transaction fees, and taxes. Returns assume the reinvestment of all distributions.
We can see that all of the approaches significantly cut down on the premium paid for protection. The “worst” performing strategy – the 63-day return z-score – had a loss of -1.0% annualized compared to the -2.3% for the constant put strategy.
Of course, just sitting in cash the entire time would have reduced the cost. The question we should ask is: how much did we forego in protection?
Below we plot the performance of these approaches over several of the larger market loss scenarios over the last 15 years.
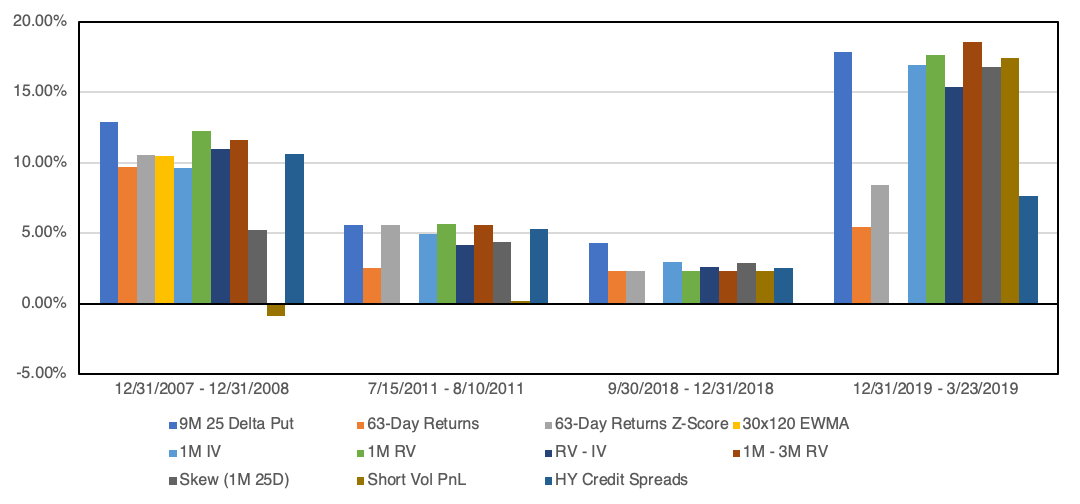
Source: DiscountOptionsData.com; Tiingo.com; St. Louis Federal Reserve. Calculations by Newfound Research. Returns are hypothetical and backtested. Returns are gross of all fees including, but not limited to, management fees, transaction fees, and taxes. Returns assume the reinvestment of all distributions.
We can see that the volatility-based models (e.g. changes in 1M IV, RV, RV – IV, and Skew) tend to do a fairly consistent job their up-capture, whereas performance-based measures on the S&P 500 (e.g. 63-day returns or 30×120 EWMA) are much less consistent. This is particularly apparent in the recent COVID-19 crisis, where return-based signals were too delayed. Interestingly, this lower upside capture was not met with decreased cost: the return-based signals were some of the worst performing models. Only the high yield credit spread model seemed to offer a balanced trade-off.
Interestingly, signals derived from a short-volatility strategy were negative in 2008. In this strategy we are short an at-the-money call and put. Calling this strategy short-volatility may be a bit of a misnomer, as it will profit when realized returns stay range-bound, which is different than explicitly generating a return from declining volatility. Nevertheless, we can see that the return profile of this approach, plotted below, looks very much like “picking up pennies in front of a steam roller.” Unfortunately, the steam roller seems to manifest rather quickly, so the 63-day return signal may be too slow in this case.
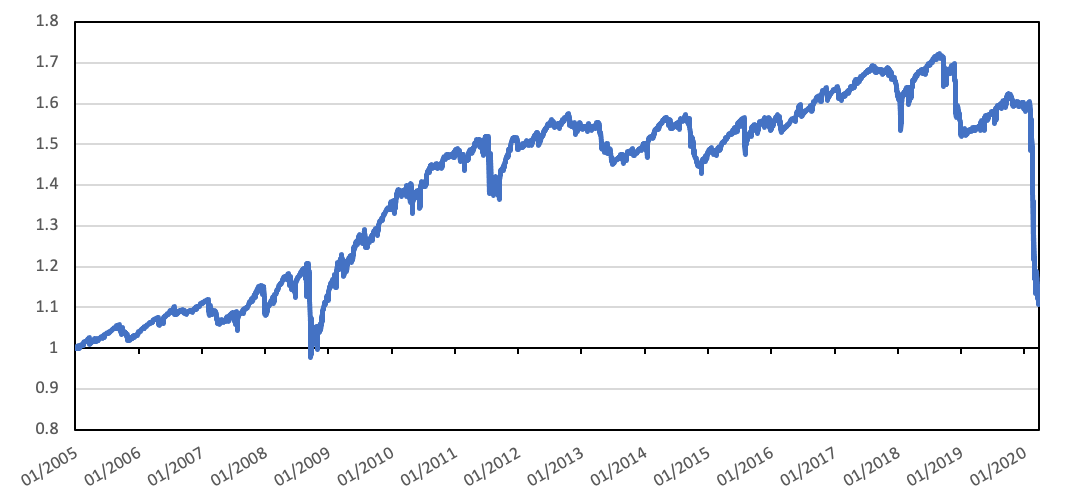
Source: DiscountOptionsData.com; Tiingo.com; St. Louis Federal Reserve. Calculations by Newfound Research. Returns are hypothetical and backtested. Returns are gross of all fees including, but not limited to, management fees, transaction fees, and taxes. Returns assume the reinvestment of all distributions.
Conclusion
Given their high certainty and degree of protection offered, put options can be prohibitively expensive (particularly after a significant market decline, when demand for protection often goes up). For investors for whom a certain level of loss is truly disruptive to operations or creates a knock-out condition, protection is not an option. For others, though, the selective use of put options may provide an interesting, diversifying payoff profile.
In this commentary, we briefly explored the application of different tactical signals to a far-dated, deep out-of-the-money put strategy. Not surprisingly, we found that all of the approaches helped reduce the annualized cost of the put strategy. However, not all of the signals provided meaningful upside capture. Given that there are few actual periods where the put strategy offers positive returns, missing these gains defeats the whole purpose of the exercise.
We found that volatility-based signals worked best. This may be due to a combination of two facts: (1) the put strategy has meaningful sensitivity to changes in implied volatility, and (2) the put strategy has an asymmetric payoff profile, reducing the cost of false positives.
These results should taken with a large grain of salt, however, as the number of meaningful payoff periods is very low. Future research should explore how these signals work when applied to different equity indices, ETFs, or even individual stocks.

