By Corey Hoffstein, Newfound Research
Recently, we were invited to speak at IMN’s Evidence-Based Investing Conference (West) on a panel about tactical allocation.
Not surprising to anyone who reads our research, our comments on the panel were largely centered around the application of systematic style premia (e.g. value, momentum, carry, and trend) to tactical allocation.
At the end of the panel, during the Q&A session, one audience member asked the question, “are there special considerations that have to be made when applying factors at the asset allocation level versus the individual security level?”
That is a question we probably could write a book about (hint: we are).
The answer is that we believe there a number of considerations that need to be made, some of which can have an outsized impact on portfolio performance if ignored. In this commentary, we want to highlight four that we believe investors should be aware of when evaluating tactical managers.
Establishing Consistent Measures Across Asset Classes
In traditional factor / style premia investing, stocks are ranked by a scoring system (e.g. valuation, past returns, et cetera). A portfolio is then built by going long the top ranked stocks (e.g. the top quintile) and short-selling the bottom ranked stocks. This approach captures the performance spread between the two baskets.
For long-only portfolios, a similar effect is achieved by overweighting the top ranked stocks and underweighting the low ranked stocks – which is, in effect, the same as “overlaying” the long/short portfolio on top of a long-only market portfolio.
When constructing factor portfolios with stocks, the scoring system works best when it can be applied across all stocks and when it provides a consistent measure to compare them to each other. For example, the traditional equity value factor is elegant because all stocks can be ranked on price-to-book and price-to-book has a consistent meaning across all stocks.[1]
The same cannot be said for asset classes: for example, bonds and commodities do not have a price-to-book metric. How then should we measure value? While we might introduce other measures (e.g. real yield for bonds), this arguably increases model risk, as we now need to validate the efficacy of several unique metrics.
Furthermore, we now need to consider how we’re going to compare metrics across asset classes. If the real yield for bonds is 2% and the price-to-book value for the S&P 500 is 3, which asset class is cheaper?
To address this problem, some sort of normalization needs to be performed (e.g. using a more consistent measure – like yield – or z-scoring), which further introduces modeling and assumption risk. Additionally, we must consider how factor scores may translate to return differentials differently across asset classes or sub-asset classes. Within fixed income, for example, the impact of similar yield and spread changes will differ across portfolios with varying durations.
Fewer “Bets” To Make
When it comes to stock picking, we tend to see two approaches to managing risk: qualitative analysis and diversification. Discretionary managers tend to prefer the former while quants tend to leverage the latter.
While we often think of a long/short factor portfolio as one basket versus another, there is no reason we cannot alternatively think of it as a large number of pairs trades, where we are long one stock and short another.
For example, consider a simple value factor that is long the cheapest 100 stocks in the S&P 500 (based upon some valuation metric) and short the 100 most expensive stocks. The return of this long/short will equivalent to the spread in performance between the two portfolios, but we can also think of it as 100 different long/short pairs: long the top ranked stock, short the bottom ranked; long the 2nd best stock, short the 2nd worst; etc.[2]
In this way, a traditional stock-based factor portfolio is diversifying across a large number of bets. Each bet, individually, has a positive expected return, but may have a large variance. By diversifying across a large number of such bets, we can reduce exposure to the idiosyncratic risks that might drive any individual pair’s performance.
When it comes to tactical asset allocation, there are typically fewer bets that can be made. While today’s strategies often have greater breadth than the stock-bond-cash strategies of yesteryear, even a 10-asset portfolio will only result in 5 long/short pairs. Without significantly dropping down the asset class hierarchy to include geographic and sector distinctions, creating internal diversification can be difficult.
Cross-Asset Dynamics
When we go long one basket of stocks and short another, we have two fairly reasonable expectations: (1) the correlation between the baskets will be fairly high, and (2) the volatility of the baskets will be similar (at the very least, in orders of magnitude).[3]
This has important implications for the risk of a factor trade. Consider that the variance of a dollar-neutral long/short portfolio will be:
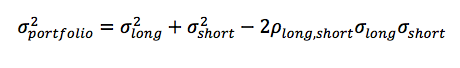
With similar variances and a high degree of correlation, we would expect the variance of the factor portfolio to be close to zero. Furthermore, both legs of the trade will, more or less, contribute to risk equally.
The same cannot be said for asset classes. Consider a naïve relative value trade that goes long stocks and short bonds.
There are a few effects to consider:
- The correlation between stocks and bonds can vary dramatically over time, leading to a shifting risk profile for the trade.
- The variance of stocks will (likely) swamp the variance for bonds, and thus the risk of the portfolio will largely be driven by what stocks do and not by what the pair does.
The relative volatility level is a particularly important effect to note. Consider a tactical trade placed with the expectation of a steepening yield curve. The curve can steepen by either a decrease in the short-end or an increase in the long-end. To play this trade, we can go long 2-year bonds and short 10-year bonds.
The problem with this trade is that 10-year bonds are much more sensitive to rate changes than 2-year bonds. If the 2-year rate falls 1% and the 10-year rate falls 0.2%, the curve has technically “flattened,” but our trade will not be profitable. For our trade to work, both legs of the trade have to have an equal amount of interest rate sensitivity (duration). Therefore, we need to buy approximately five 2-year bonds for each 10-year bond we short.[4]

