Since matrix multiplication dominates the overall computation (77% of overall compute time when B=128, N=3072, and L=2), we also analyzed the achieved FLOP/s for that operation. As shown in Figure 2, we found the performance trend for matrix multiplication is similar to the end-to-end performance discussed above. We achieved a peak of 75.1 TFLOP/s using mixed precision techniques, a performance boost of 5.3X compared to peak achieved, 14.1 TFLOP/s using single precision numbers. Figure 2 shows the details trend for 2 layers word language model varying batch size and the number of LSTM cells. Contrast to end-to-end application, we see that the slope for matrix multiplication using FP32 starts saturating earlier (at batch size of 128). For mixed precision, the trend seems similar and the rate slows down at batch size of 256. We observed similar performance gain for matrix multiplication when we increased the number of layers to 3-5. For the matrix multiplication operation, we found the peak utilization to be 89% and 60% for FP32 and mixed precision, respectively.
![]()
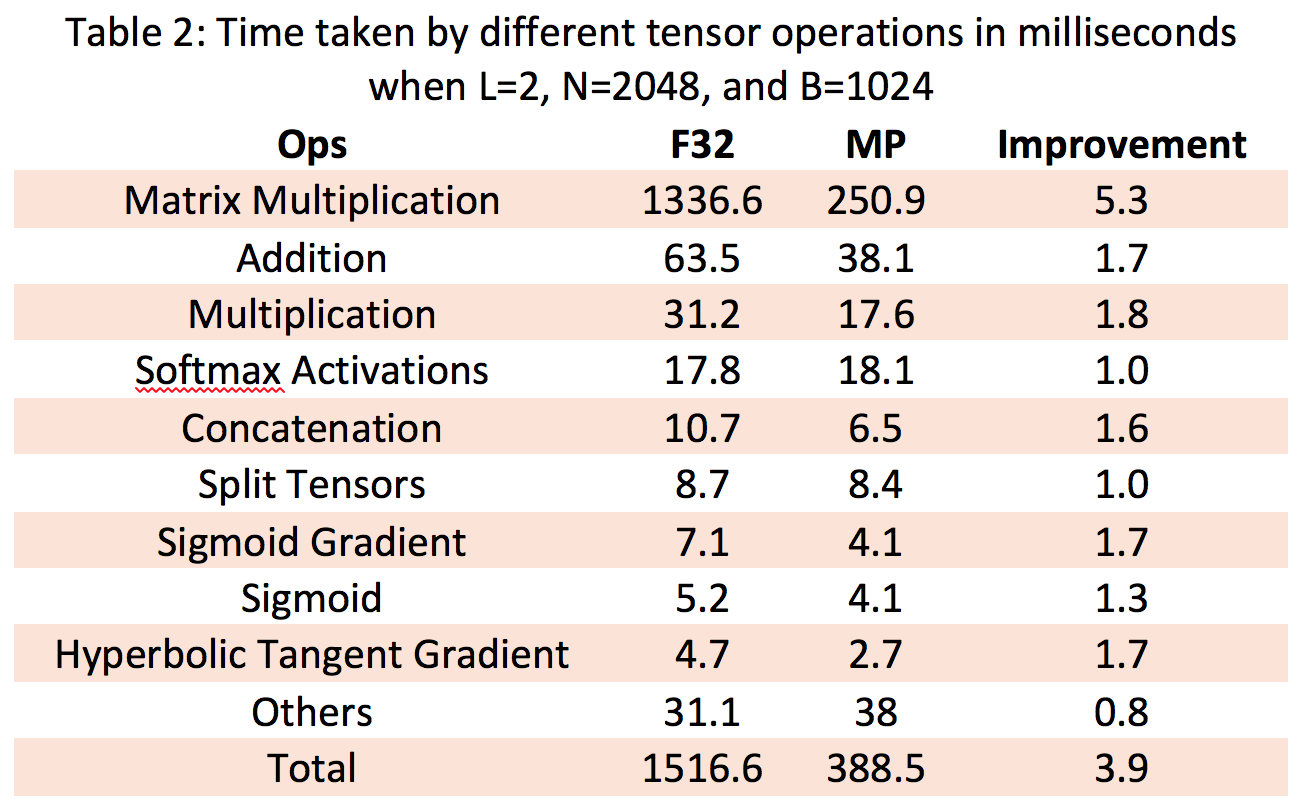
Table 2 shows the performance breakdown for each tensor operation (Op) for word language models for FP32 and mixed precision training. We only listed the tensor Ops that take 0.25% or higher of the total compute time. The rest of the Ops are summed as others in the table. As can be seen, matrix multiplication and addition are the dominant operations (88% and 4% of total, respectively for FP32) in word language model. We found 5.3X gain for matrix multiplication using mixed precision numbers. We attribute the gain to the TensorCore hardware in V100, which showed 75.1 TFLOP/s (60% utilization of peak FLOP/s) for matrix multiplication. In case of addition, a memory bound operation, we achieved 1.7X performance gain with utilization of 71% (638 GB/s) of the peak memory bandwidth (900 GB/s). We see similar utilization and gain for other memory bound operations using mixed precision such as Concatenation and Multiplication compared to single precision numbers.
We also investigate how cuDNN LSTM cells in the recurrent layers perform on mixed precision compared to basic LSTM cells [5]. We found that cuDNN LSTM shows up to 1.9X speedup compared to basic LSTM based implementation. We also observed that the speedup is much higher when the batch size is small (e.g. speedup of 1.9X at batch size 32); as the batch size increases, the speedup reduces (e.g. speedup of 1.5X and 1.1X for batch size of 256 and 1024, respectively). We attribute the higher performance of cuDNN LSTM cells to fusing element-wise operations and overlapping computations from different layers and timesteps. However, we were unable to use the cuDNN implementation in the above experiments because of autoregressive data dependencies and small LSTM cell differences that we have found contribute to non-trivial differences in accuracy.
To summarize, we achieved 4.1X performance improvement end-to-end for word language models using mixed precision technique compared to single precision numbers. The performance gain attributes to the FP16 arithmetic in faster hardware like V100 and low memory requirement in the mixed precision technique. We observe increasing the batch size and number of hidden nodes increases the performance proportionally. However, we observe that the performance gain independent of the number of layers used in the model. We also observe that the achieved utilization by mixed precision is much lower than FP32. Considering accuracy, we found that with a tuned value of the loss-scaling parameter, S, accuracy using mixed precision matches the baseline accuracy of FP32.
Authors: Mostofa Patwary, Sharan Narang, Eric Undersander, Joel Hestness, and Gregory Diamos
Acknowledgment: We would like to thank Michael Andersch from NVIDIA for valuable discussion on the mixed precision implementation and also the contribution on experiments comparing Basic LSTM vs CuDNN LSTM cells.
Reference:
1. Mixed Precision Training, Sharan Narang, http://research.baidu.com/mixed-precision-training/
2. Mixed Precision Training, Paulius Micikevicius, Sharan Narang, Jonah Alben, Gregory Diamos, Erich Elsen, David Garcia, Boris Ginsburg, Michael Houston, Oleksii Kuchaiev, Ganesh Venkatesh, and Hao Wu, http://lanl.arxiv.org/abs/1710.03740
3. Mixed Precision Training of Deep Neural Network, Paulius Micikevicius, https://devblogs.nvidia.com/mixed-precision-training-deep-neural-networks/,
4. Exploring the Limits of Language Modeling, Rafal Jozefowicz, Oriol Vinyals, Mike Schuster, Noam Shazeer and Yonghui Wu, https://arxiv.org/abs/1602.02410
5. S. Hochreiter and J. Schmidhuber. “Long Short-Term Memory”. Neural Computation, 9(8):1735-1780, 1997, http://www.bioinf.jku.at/publications/older/2604.pdf
