Model error improves starting with “best guessing” and following the power-law curve down to “irreducible error”.
More generally, our empirical results suggest that learning curves take the following form (Again, log-log scale!):
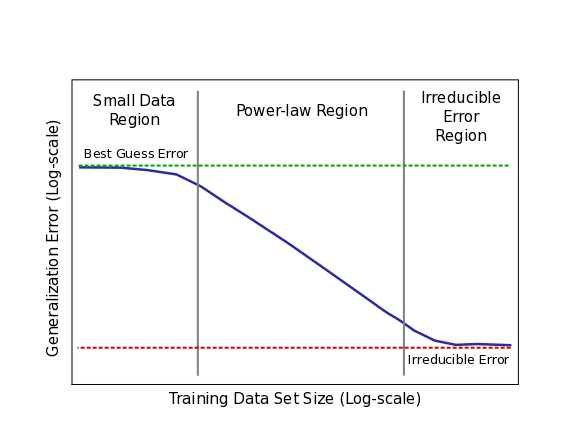 Sketch of power-law learning curves for real applications
Sketch of power-law learning curves for real applications
The figure above shows a cartoon sketch power-law plot that breaks down learning curve phases for real applications. The curve begins in the small data region, where models struggle to learn from a small number of training samples. Here, models only perform as well as “best” or “random” guessing. The middle portion of learning curves is the power-law region, where each new training sample provides information that helps models improve predictions on previously unseen samples.
The power-law exponent defines the steepness of this curve (slope when viewed in log-log scale). The exponent is an indicator of the difficulty of understanding the data. Finally, for most real world applications, there is likely to be a non-zero lower-bound error past which models will be unable to improve (we have yet to reach irreducible error on our real-world tests, but we’ve tested that it exists for toy problems). This irreducible error is caused by a combination of factors inherent in real-world data.
Across the applications we test, we find:
- Power-law learning curves exist across all applications, model architectures, optimizers, and loss functions.
- Most surprisingly, for a single application, different model architectures and optimizers show the same power-law exponent. The different models learn at the same relative rate as training set size increases.
- The required model size (in number of parameters) to best fit each training set grows sublinearly in the training set size. This relationship is also empirically predictable
We hope that these findings can spark a broader conversation in the deep learning community about ways that we can speed up deep learning progress. For deep learning researchers, learning curves can assist model debugging and predict the accuracy targets for improved model architectures. There is opportunity for redoubled effort to theoretically predict or interpret learning curve exponents. Further, predictable learning curves can guide decision-making about whether or how to grow data sets, system design and expansion, and they underscore the importance of continued computational scaling.
More details and data can be found in our paper: Deep Learning Scaling is Predictable, Empirically
The following article was republished with permission by Baidu Research.
